-
[알고리즘 문제 풀이][세그먼트트리] 백준 3392번 - 화성 지도자료구조&알고리즘/알고리즘 - 대회 알고리즘 2022. 2. 28. 17:40
백준 3392번 화성 지도 문제입니다.
(세그먼트 트리 & 스위핑)
- 문제 설명: https://www.acmicpc.net/problem/3392
- 문제 풀이:
본 문제는 다른 블로그들의 풀이를 참고하여 풀었기 때문에, 기존 풀이 방식과 동일합니다.
본 문제는 세그먼트 트리를 공부하기 위해 풀게 되었는데, 세그먼트 트리의 기초 개념만 알면 풀 수 있었던 문제들과 달리, 본 문제는 어느 부분에 세그먼트 트리를 적용해야할 지 어려운 문제였습니다.
일반적인 풀이는 들어온 입력들을 정렬을 하고, 쭉 스캔을 하면서 스캔한 범위에 사각형의 일부가 들어있으면 그걸 다 합하는 방식입니다. 이때 스캔한 범위에 사각형 선이 들어있는지 아닌지를 세그먼트 트리로 관리합니다.
들어온 입력을 보면 아래와 같습니다. 사각형 두 개가 들어오고, 겹치는 영역이 존재합니다.
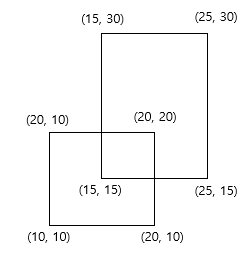
이 입력을 이런 방향으로 스캔하고자 합니다. (이렇게 한번 훑으면서 구하는 것을 스위핑 알고리즘이라고 합니다)
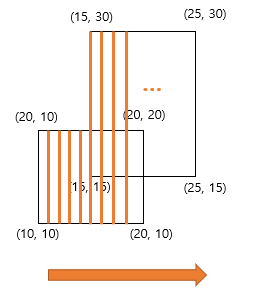
그런데 사실 x가 10일 때, 11일 때, 12 일 때, ... 이 값을 다 일일히 계산할 필요는 없습니다. x가 10일 때부터 15이기 전까지는 높이가 다 같기 때문입니다. 입력으로 들어오는 x 에 대해서만 관리하면 답을 구할 수 있습니다.
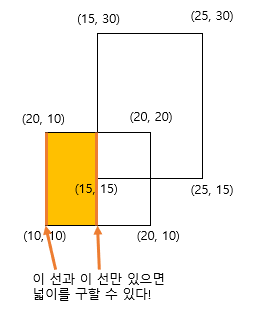
들어오는 입력은 x1, y1, x2, y2 로, (10, 10, 20, 20) 과 (15, 15, 25, 30) 이므로, x를 정렬하면 10, 15, 20, 25 가 나옵니다. 이 범위에 대해서 넓이를 구하면 됩니다.
그러면 이제 특정 x 를 찾았을 때 존재하는 y 를 구해보겠습니다. 세그먼트 트리를 그냥 이용하면 특정 구간의 합을 구할 수 있을 것입니다. 그러나 여기서는 사각형이 겹쳐있기 때문에 존재한다고 해서 다 합해버리면 사각형의 길이가 실제보다 더 길게 구해질 수가 있습니다.
따라서 많은 분들이 사용한 트릭을 똑같이 사용하였습니다. cnt 배열에 해당 구간이 지금 유효한지 아닌지 (유효하면 1 이상, 유효하지 않으면 0) 표시를 해서 구간 합을 구하는 것입니다. 유효하면 값이 몇 이든 상관 없이 그냥 y 범위를 리턴합니다. (end - start + 1) 을 리턴합니다. 그러면 중복을 고려할 필요가 없어집니다.
cnt 업데이트 방법은 아래와 같습니다.
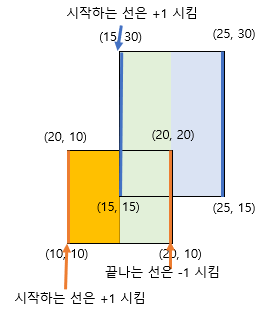
시작하는 선은 구간에 들어가도록 cnt 에 +1 을 해주고, 끝나는 선은 지금을 지나면 더 이상 구간이 잡히지 않도록 cnt 에 -1 을 해줍니다. 그러면 중간에 x = 15 인 지점은 아래 사각형의 선도 +1된 상태, 위의 사각형도 +1 된 상태로 cnt 가 1보다 커질 수도 있는데, 코드에서 답을 구할 때 cnt 가 아닌 segment 배열에서 end-start+1 한 결과값으로 리턴할 것이기 때문에 문제가 없습니다.
- 코드:
############################################### # segment tree ############################################### def update(node, start, end, left, right, val): if end < left or start > right: return if left <= start and end <= right: cnt[node] += val # start +1, end -1 else: mid = start + (end-start)//2 update(node*2, start, mid, left, right, val) update(node*2+1, mid+1, end, left, right, val) # cnt = 0 # default value if cnt[node] > 0: seg[node] = end - start + 1 else: # leaf node 는 합도 0 # if s == e 처리 해주면 seg, cnt 크기 *2 안 필요 seg[node] = seg[node*2] + seg[node*2+1] seg = [0] * 30001*2*4 # the total number of points in section not including overlap cnt = [0] * 30001*2*4 # the total number of points in section, including overlap, 0 = no point, >1 = points exist ############################################### # input & sort ############################################### my_map = [] N = int(input()) for _ in range(N): x1, y1, x2, y2 = map(int, input().split()) my_map.append((x1, y1, y2-1, 1)) # start my_map.append((x2, y1, y2-1, -1)) # end my_map.sort() # sort based on x ############################################### # sweep by using segment tree ############################################### ans = 0 # first x x, y1, y2, val = my_map[0] update(1, 0, 30000, y1, y2, val) # val = start or end # from second x for i in range(1, N*2): x_diff = my_map[i][0] - my_map[i-1][0] ans += x_diff * seg[1] # the total number of points update(1, 0, 30000, my_map[i][1], my_map[i][2], my_map[i][3]) print(ans)- 실수 포인트 & 반례:
1. 런타임 에러: 세그먼트 트리를 이용하는 경우, 배열 크기가 충분한지 확인해야합니다. (정확히 잡으면 (1 << (ceil(log2(N)) + 1) ) 이고, 메모리 공간이 충분한 경우, 약식으로 잡을 때는 N * 4 입니다)
(참고) https://yabmoons.tistory.com/431
반응형'자료구조&알고리즘 > 알고리즘 - 대회 알고리즘' 카테고리의 다른 글
[알고리즘 문제 풀이][유니온파인드] 백준 20040번 - 사이클 게임 (0) 2022.07.08 [알고리즘 문제 풀이][재귀] 백준 11729번 - 하노이 탑 이동 순서 / 1914 번 - 하노이 탑 (0) 2022.03.01 [알고리즘 문제 풀이][DP] Leetcode 264번 - Ugly Number II (0) 2022.02.19 [알고리즘 문제 풀이][기하학] 백준 3053번 - 택시 기하학 (0) 2022.02.15 [알고리즘 문제 풀이][완전탐색] 백준 12784번 - 인하니카 공화국 (0) 2022.02.13 댓글