백준 2545 팬케익 먹기 증명 (라그랑주 승수법)
수학 무지렁이의 증명 노트
2024.04.14
1) 문제
백준 2545번 팬케익 먹기 문제
https://www.acmicpc.net/problem/2545
2545번: 팬케익 먹기
두 번째 테스트 케이스를 보자. 왜 정답이 64일까? 가장 먼저 4 * 5 변에 맞춰서 2번 팬케익을 자르면 남은 팬케익은 4*5*4가 된다. 그 다음에 4 * 4 변에 맞추어 팬케익을 자르면 4*4*4가 된다. 따라서 6
www.acmicpc.net
박스 모양의 팬케익의 가로 세로 높이가 각각 A cm, B cm, C cm 일 때 D번 자르고 남은 부피를 최대화 하는 방법
A, B, C 를 각각 어떻게 값을 줄여야 A*B*C 가 최대가 되는지 찾는 문제
요약하면,
x+y+z = c 로 일정할 때 x*y*z 를 최대화하기 (c는 상수, x, y, z 는 0 보다 큰 정수)
2) 증명 시도
(1) [손으로 찾기] 직관적으로 어떤 식이어야 남은 수의 곱이 최대가 되는지 계산해보면
x, y, z 가 최대한 값이 비슷해야 제일 값이 커졌다.
예를 들어 x+y+z = 6이라면 x=1, y=1, z=4 면 x*y*z = 4 이지만, x=3, y=3, z=3 이라면 x*y*z = 27 이 나온다. 손으로 수들을 직접 써보니 최대한 비슷한 수일 때 값이 가장 커졌다. (이렇게 알아내고 일단 문제는 맞추긴 했다...)
(2) [이차함수] 값이 2개일 때를 생각해보면 증명할 수 있었다.
x+y = c 라면, y = c-x 라고 볼 수 있다.
따라서, x*y 를 x*(c-x) 로 변환할 수 있다.
그러면 -x^2 + cx 로 이차식이 된다.
이를 이차함수처럼 생각해볼 수 있다. (y 를 다시 써서 헷갈릴 수 있지만, 이차함수의 y 로 위와 다른 의미로 썼다.)
y = -(x-c/2)^2 + c^/4 로 보면,
위로 볼록한 이차함수의 y 최댓값은 꼭짓점이 된다. (오른쪽 그림)

[이미지 출처] https://thebook.io/080246/0041/
위에 정리된 식에 따르면 이차함수의 꼭짓점은 x = c/2 일 때이며, 이 때의 y 값 또한 y = c/2 가 된다.
따라서 값이 2개일 때는 둘 다 평균값에 가까울수록 최댓값이 된다고 할 수 있다.
하지만 지식의 한계로 3개일 때로 확장할 수는 없었다...
(3) [AM-GM 부등식] chatGPT 에게 어떻게 최적화할 수 있는지를 물어보았더니, 라그랑주 승수법, AM-GM 부등식, 수치적 최적화 알고리즘을 추천해주었다. AM-GM 부등식 (Arithmetic Mean-Geometric Mean Inequality) 는 아래와 같이 평균한 값이 루트를 씌운 값보다 무조건 크거나 같다는 식이다.
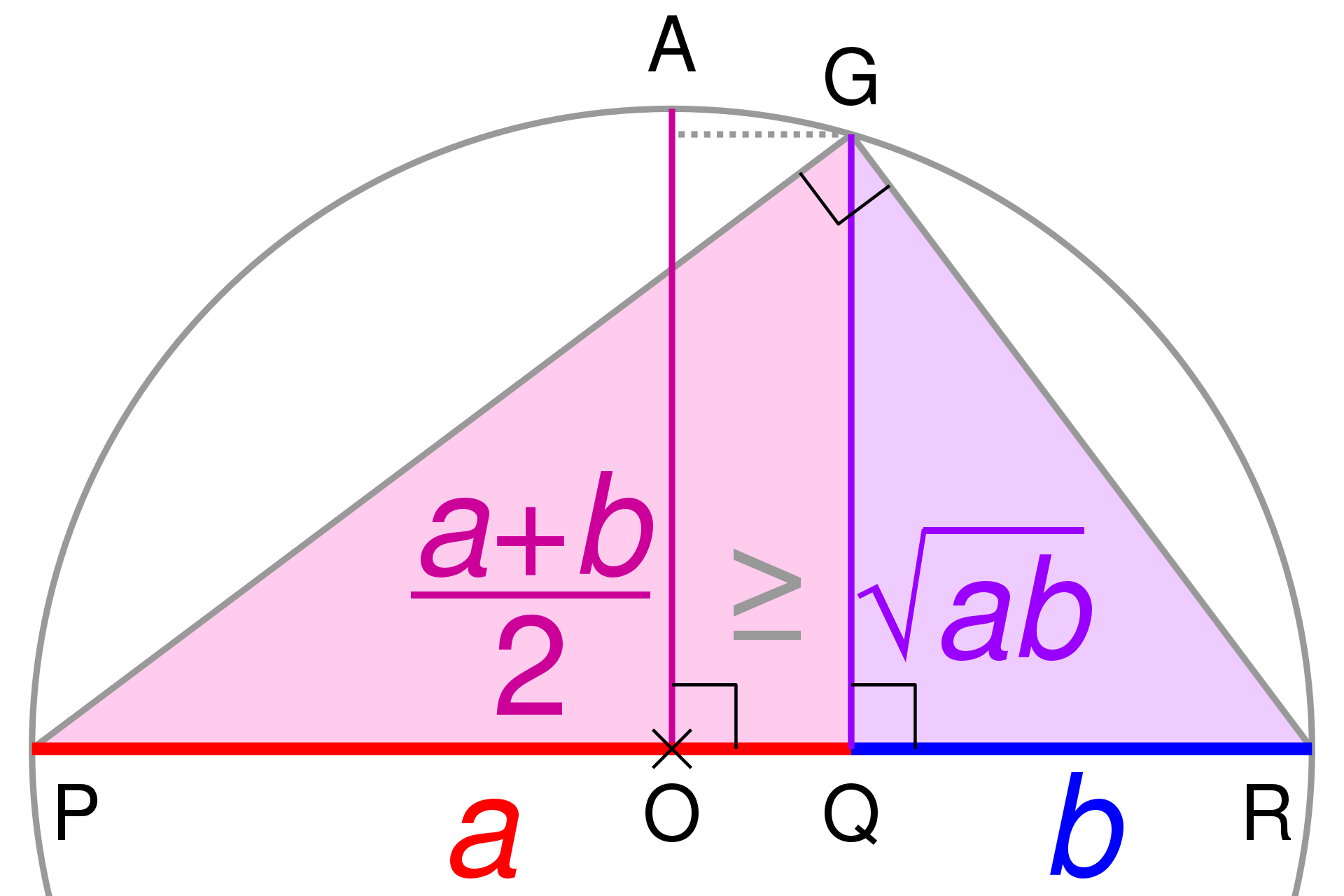
이는 n 에 대해서도 성립한다.
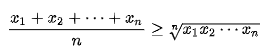
즉, (x+y+z) / 3 >= ³√(x*y*z) 도 성립한다는 것이다.
그렇다면 x*y*z 의 최댓값은 (c/3)^3 이 된다...!
이 값을 만들려면 x, y, z 모두 c/3 이 되면 최댓값을 (c/3)^3 을 만들 수 있다. x+y+z = 9 라면, x*y*z 의 최댓값은 27이 되는 것이다. 그러면 x=y=z=3 이라고 계산할 수 있다.
그러면 만들 수는 있는데... 최댓값만 알아낸 걸로 무조건 x=y=z=c/3 이라는 깔끔한 증명이 된 것이 맞는지 뭔가 하나가 빈 것 같은 느낌이 든다...
(4) [라그랑주 승수법] chatGPT 에게 라그랑주 승수법으로 증명하는 과정을 알려달라고 했다.
* 라그랑주 승수법을 쉽게 이해하도록 도와주는 블로그를 찾아봤지만... 한번 보고서 이해가 되진 않았다...ㅠ
아직 라그랑주 승수법을 이해하진 못했지만, 나중에라도 이해할 수 있으므로 일단 정리해둔다.
라그랑주 승수법은 제약 조건이 있는 최적화 문제를 해결하는데 사용된다. 제약 조건과 목적 함수 (최대화 또는 최소화해야하는 함수) 를 함께 고려하여 라그랑주 함수를 만들고, 이 함수를 편미분하여 최적해를 찾는다.
1) 우선 라그랑주 함수를 정의한다.
L(x, y, z, λ) = x*y*z - λ(x+y+z-c)
여기서 λ 람다는 라그랑주 승수이다.
2) 각 변수에 대해 편미분하고, 도함수가 0이 되는 조건을 찾는다.
∂L/ ∂x = y*z - λ = 0
∂L/ ∂z = x*y - λ = 0
∂L/ ∂y = x*z - λ = 0
3) 위 식을 풀면, x = y = z 가 된다.
그리고 제약 조건에 의해 x+y+z = c 이므로, 3x = c 가 된다.
따라서 x = y = z = c/3 이 된다.